
文|常涧滕
编辑|常涧滕
介绍
如今,原油价格预测在全球能源和经济系统中的重要作用已成为数据分析和预测中的一个有吸引力的问题,原油价格与其他大宗商品一样,受供需等市场因素影响较大,原油价格预测已变得越来越具有挑战性。

本文着重于通过减少随机不确定性来高精度地预测原油价格。
在过去的二十年中,典型的统计工具和计量经济学方法被用于预测原油价格,例如广义自回归条件异方差(GARCH)模型,自回归移动平均(ARIMA)模型,线性回归,朴素随机游走、纠错模型(ECM)和向量自回归(VAR)模型。
与单一模型相比,基于分解和集成策略的模型可以很好地模拟原油价格复杂数据,由于分解过程,由于时间序列被分解成多个独立模式,模型复杂性、计算时间和成本会产生另一个问题。
为了进一步提高预测效率和有效性,使用从EEMD获得的分解模式的新方法,遵循众所周知的“分解与集成”框架,提出了一种利用重构模型预测原油价格的新方法。
研究框架
研究中使用的框架或步骤如下:
1.使用EEMD技术将原始时间序列分解为IMF
2.IMF根据其影响分为两部分,即基于AMI的随机和确定性
3.使用Box-Jenkins方法为每个随机IMF和确定性组件选择最佳ARIMA模型,并获得用作KF模型输入的参数估计值,每个随机IMF和确定性成分的KF模型的输出被简单地相加以获得预测值。
4.最后,比较预谋的方法以检查哪个模型提供更准确的预测。
集成EMD(EEMD)
Wu和Huang 介绍了著名分解技术的新版本,即EMD,它最初是由通过向调频参数添加一些噪声而开发的。
- 在每个提取信号的完整长度上,过零数和极值数之差不得超过1。
- 由下包络和上包络定义的任何点处的信号平均值将始终等于零。
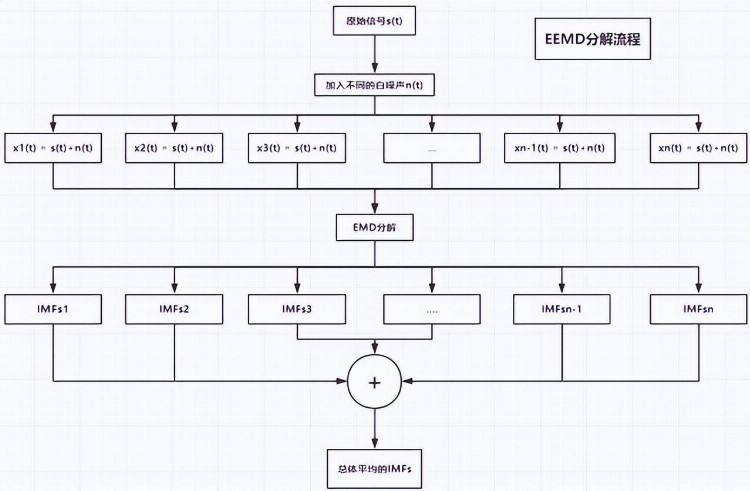
图1
保留这两个限制,可以从原始信号中提取有意义的IMF,原始时间序列 Yt可以通过简单地添加所有IMF来从分解的组件中轻松获得,如下所示:

使用EMD技术的特性,EEMD过程可以描述如下:
- 将白噪声系列添加到目标数据中。
- 获得来自添加的白噪声数据的IMF。
- 对于不同的白噪声系列,每次重复步骤(1)和(2)。
- 因此,获得了分解序列的系综对应的IMF。
ARIMA模型
从过去五十年开始,Box-Jenkins过程是分析时间序列应用程序的常用方法,最初由Box和Jenkins 提出; ARIMA模型的表达式如等式(2)所示。
αi , βi表示ARIMA模型的参数,εt 是均值和方差为零的白噪声过程,σ2 .εt - i 表示先前的误差项,而p和q是各自项的顺序。
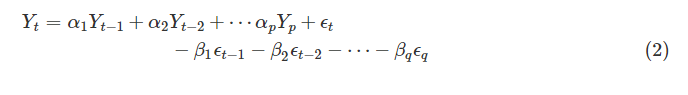
未重构的EEMD-ARIMA模型
EEMD-ARIMA模型使用从EEMD获得的所有IMF,该模型也称为不带重建分解集成(RDE)模型,在这种技术中,所有IMF都被建模并用于预测目的,EEMD-ARIMA过程可以总结为以下三个步骤。
- 分解了原来的时间序列Yt(t=1,2,⋯T) 进入n 组件(IMF)我米Fj( t ) ( j = 1 , 2 , ⋯ , n ) 。
- 为所有提取的IMF选择最佳ARIMA模型,并对相应的序列建模,并对每个序列进行预测。
- 最后将所有IMF的预测结果相加,得到目标时间序列的输出。
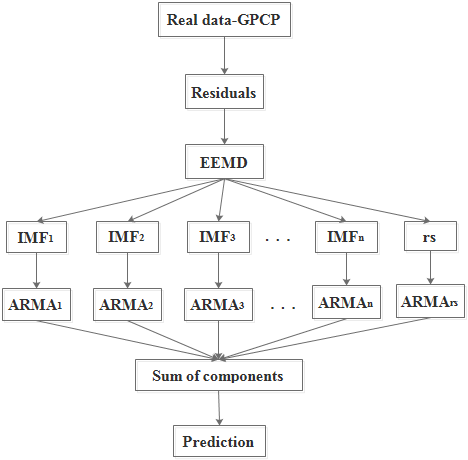
无RDE模型(即EEMD-ARIMA和EEMD-ARIMA-KF)的流程图如图2所示。
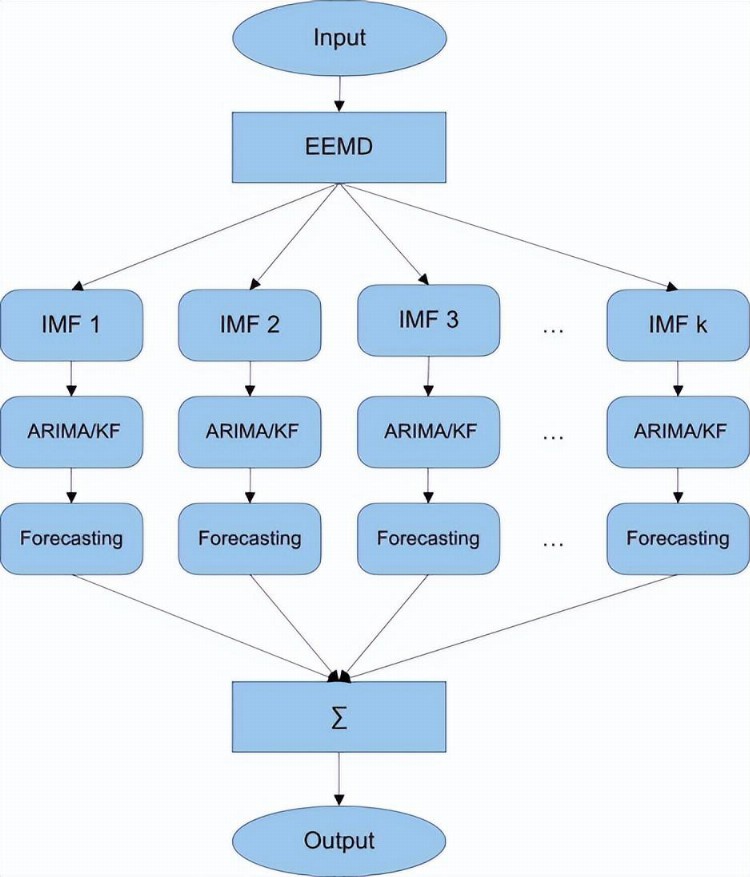
图2 无RDE模型的流程图
预测评价标准
本研究中提出的模型EEMD(SD)-ARIMA-KF的预测能力应使用六个不同的标准来衡量,并定义如下:
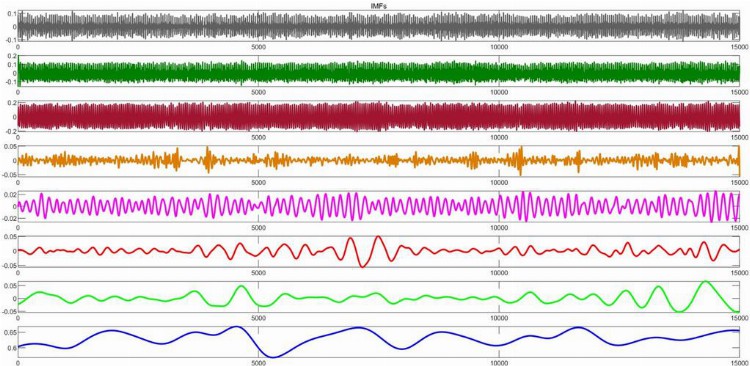
均方根误差(RMSE)
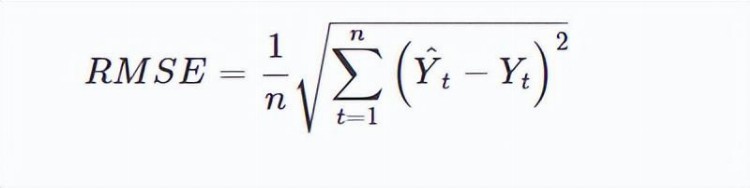
平均绝对误差(MAE)

平均绝对百分比误差(MAPE)
n 代表预测总数,Y^t 用于预测值和Yt 用于给定时间的原始值,上面提到的三种方法在预测精度上比较常见,但是这些方法只衡量预测的水平,而不衡量预测的方向。
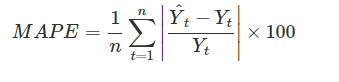
数据信息
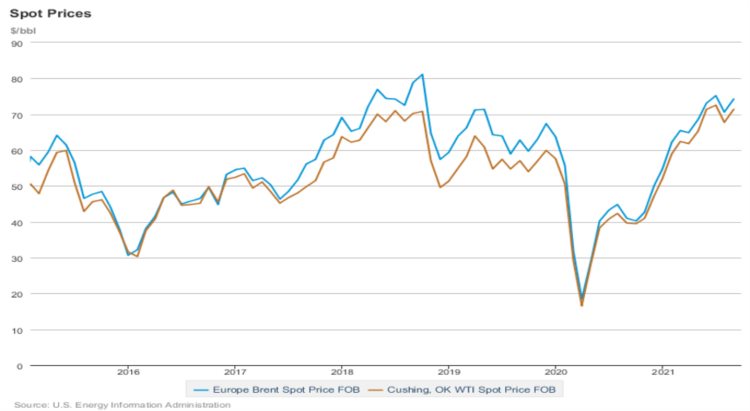
在本文中,使用了两个众所周知的基准价格的原油日价格数据,即布伦特和WTI数据集,这些数据集是从汤森路透运营的DataStream中收集的。
布伦特原油价格的第一个数据集涵盖了将近39个日历年(1970年2月2日至2008年5月29日),总共9999个观测值用作训练。
另外八年的原油价格数据(2008年5月30日-2016年11月3日)共保留2200个观测值用于测试,第二个数据集是WTI原油价格,涵盖了27个日历年(1983年1月11日至2010年8月15日)共7200个观测值用作训练。
EEMD模型
EEMD取决于直接影响此过程性能的两个参数,应在使用EEMD之前固定,这两个参数是合奏的数量和白噪声的幅度。
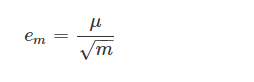
EEMD技术在这项工作中采用了上述描述,并相应地在不同的IMF中分解了两个原油系列,
R包“Rlibeemd”用于这项工作中的数据分解,两种原油价格的分解结果如图4和图5所示。
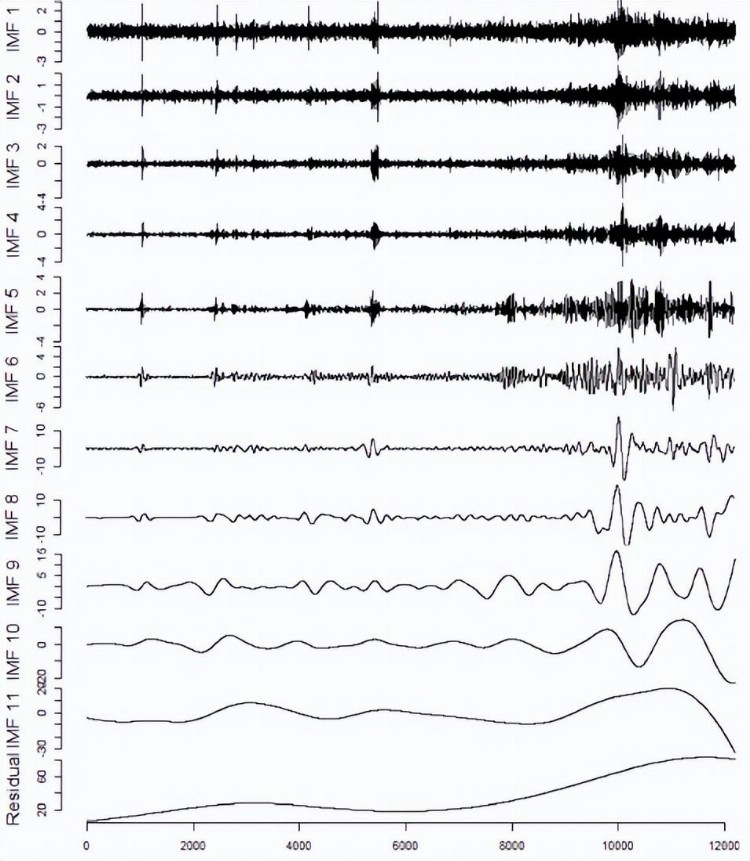
图4 布伦特原油价格分解结果
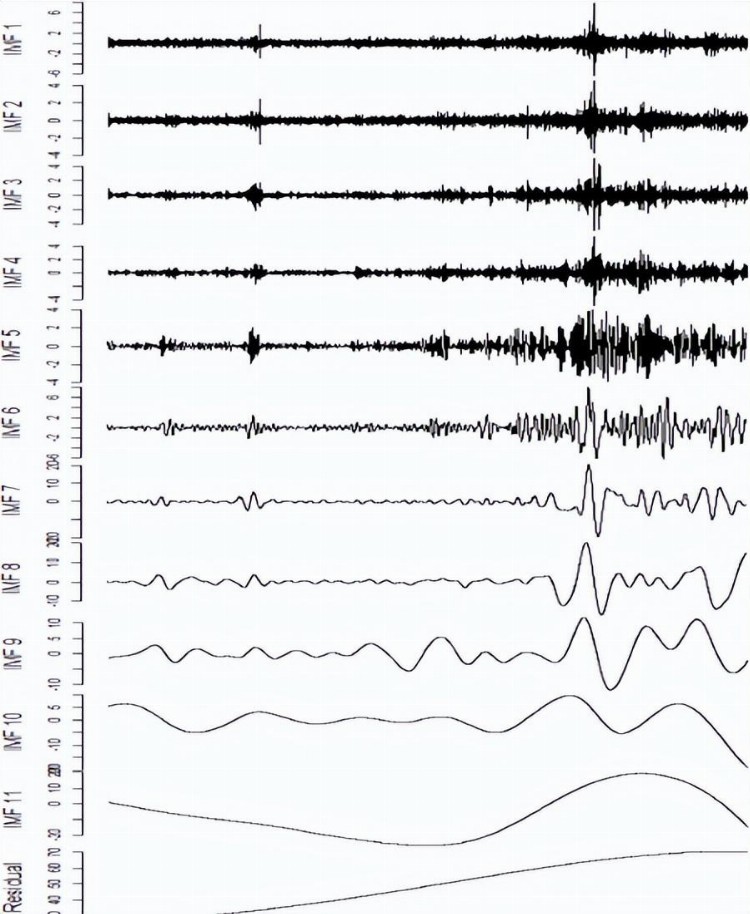
图5 WTI原油价格分解结果
在本节中,将计算单个模型作为基准,计算了布伦特和WTI原油价格的最佳ARIMA模型,布伦特系列的最佳选择模型是ARIMA(5,2,0),而对于WTIARIMA(3,1,2),R包预测用于ARIMA模型选择和计算。
表1的值证明ARIMA和GARCH模型的所有参数对于布伦特和WTI原油价格系列在1%的显着性水平上具有统计显着性。
为便于比较,布伦特和WTI原油价格序列的预测准确度均列于表5。
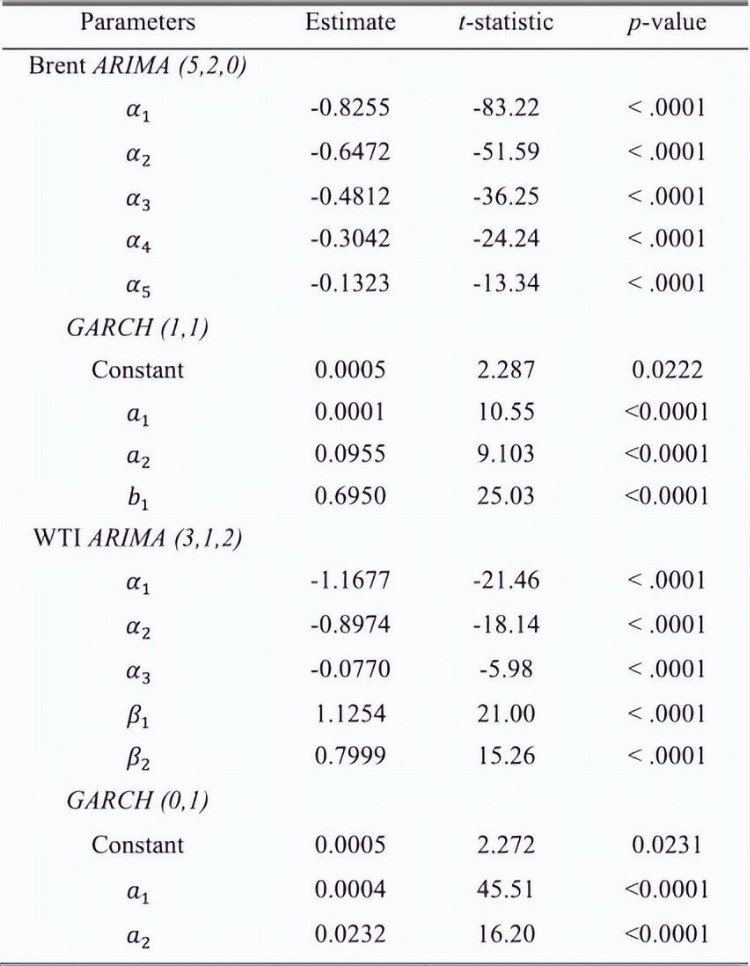
表1 ARIMA和GARCH模型估计
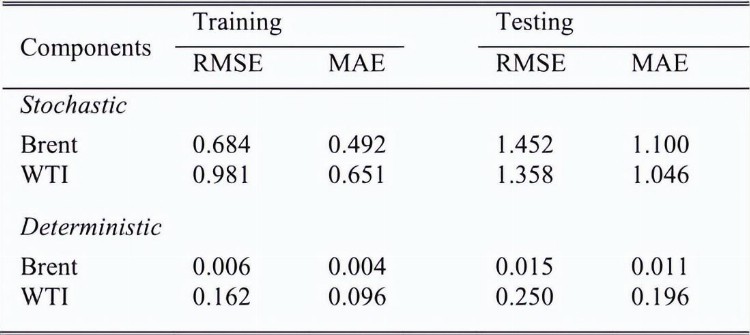
表2 随机和确定性成分的预测准确性

表3 布伦特和WTI的所有IMF的ARIMA模型阶数

表4 每个随机IMF、确定性和随机分量的KF递归的初始值
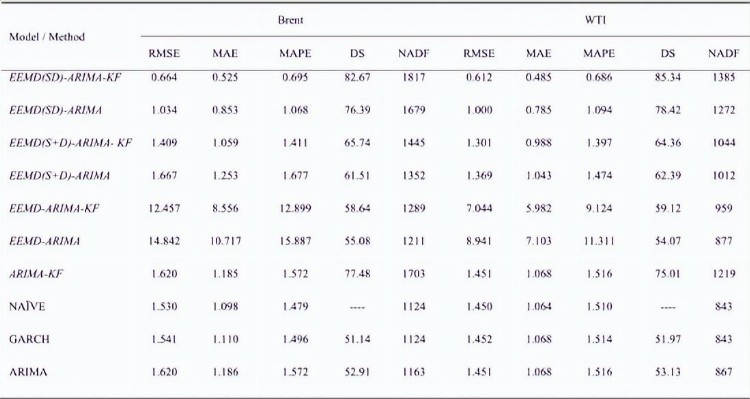
表5 不同模型的预测精度
平均互信息
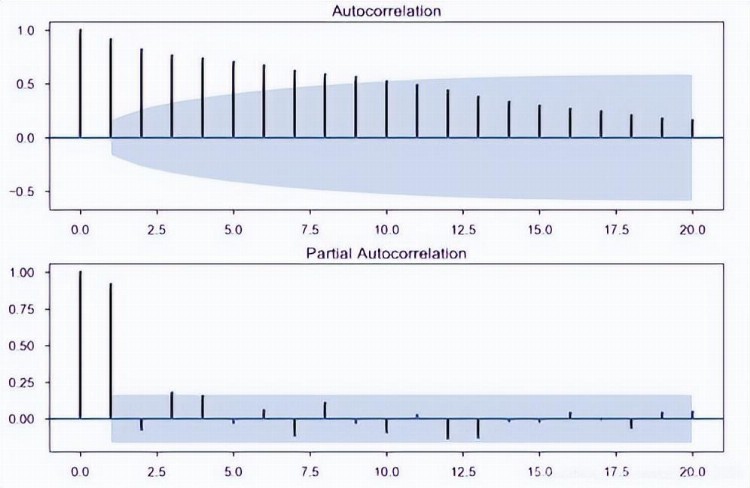
EEMD以第一个IMF与下一个IMF相比具有最大频率的模式生成IMF,反之亦然;因此,EEMD通过去除从高频到低频的分量,起到频率滤波器的作用。
所有IMF的AMI图分别显示在图6和图7中,从图6和图7的目视检查中可以看出,AMI的图在第5个IMF到最后一个IMF之后遵循相同的模式。
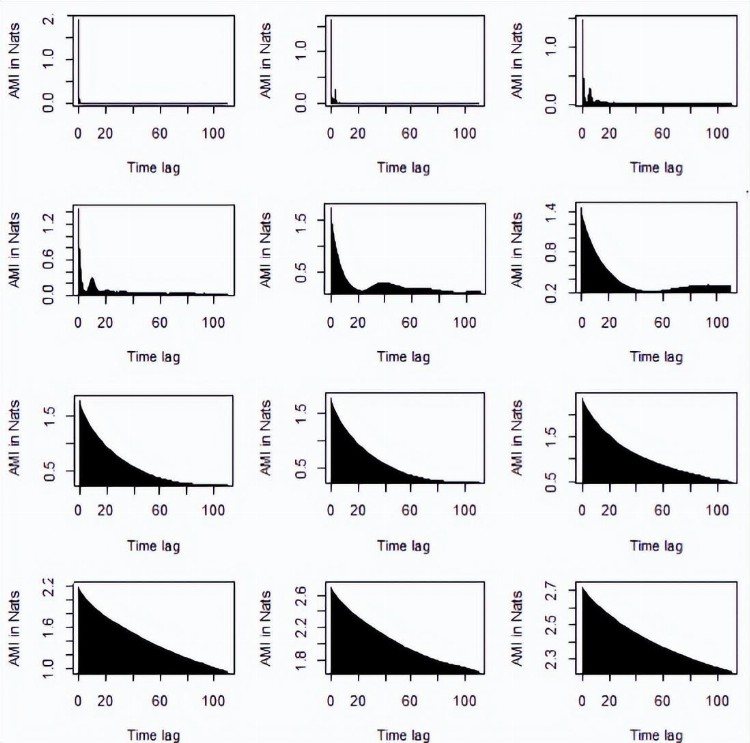
图6 布伦特原油价格的所有IMF的AMI图
图7 WTI原油价格的所有IMF的AMI图
对于随机分量,组合所有随机IMF,而对于确定性分量,将所有确定性IMF相加,布伦特和WTI数据集的这两个分量如图8和图9所示。
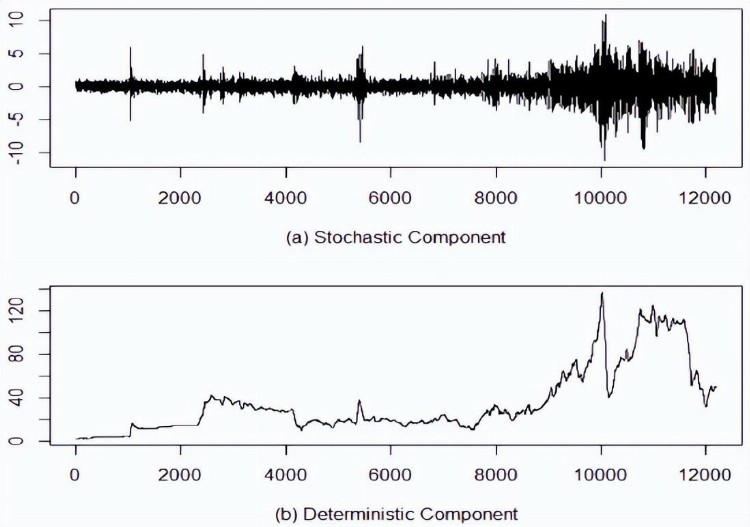
图8 布伦特原油的随机和确定性成分
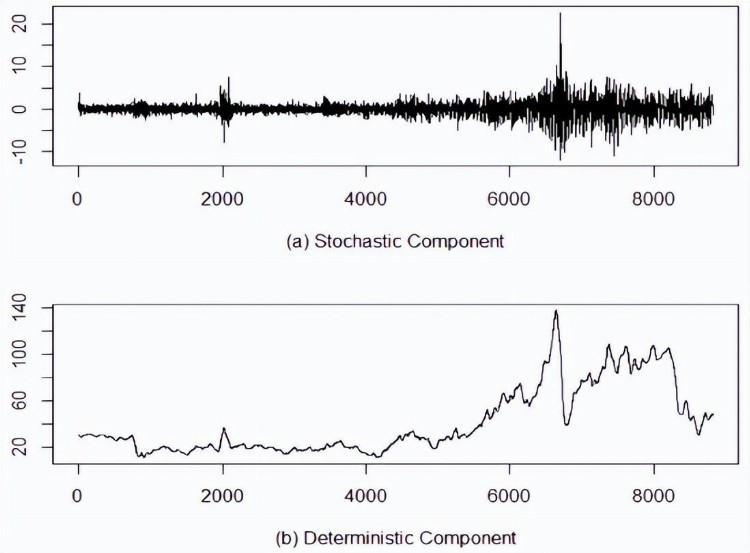
图9
ARIMA-KF模型
一旦对所研究的时间序列执行了ARIMA建模,就可以创建ARIMA-KF模型,当实现数据的平稳性时,将Box-Jenkins方法应用于时间序列。
布伦特和WTI原油价格的SE和OE被初始化,KF递归用于原油价格预测,KF递归的SE结合了ARIMA模型的线性和非线性成分;由于线性和非线性成分的结合有助于提高原油价格预测的准确性,并能够处理原油价格数据中的随机不确定性,OE表示拟合序列,也用于测量预测误差。
EEMD(S+D)-ARIMA-KF模型
预测原油价格的方法是基于卡尔曼滤波器的随机和确定性分量的EEMD,时间序列通过EEMD分解为IMF,接下来使用AMI方法将IMF划分为随机和确定性成分,表3显示了从两种原油价格的EEMD获得的所有IMF的ARIMA模型的顺序,对于EEMD-ARIMA模型,使用了ARIMA模型的这些阶数,模型EEMD-ARIMA也称为没有RDE模型。
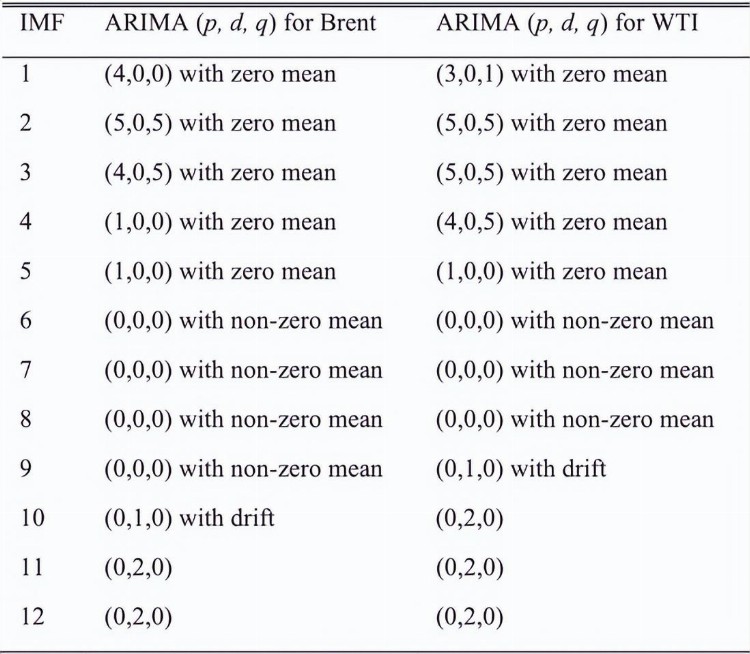
表3 布伦特和WTI的所有IMF的ARIMA模型阶数
EEMD(SD)-ARIMA-KF模型
为了减少重构IMF的随机分量中的随机性,我们分别对每个IMF进行建模,作为随机分量的一部分;预计与将所有随机IMF作为单个组件处理相比,对随机IMF单独建模将提供更准确的预测。
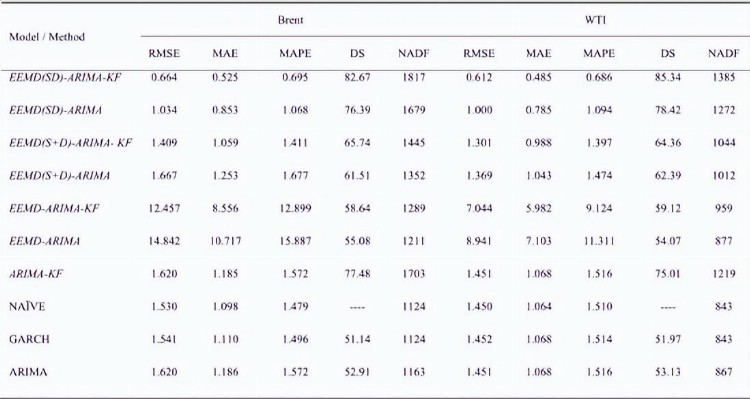
表5 不同模型的预测精度
结果讨论
为了评估所提出模型EEMD(SD)-ARIMA-KF的性能,采用了六种定量性能评估措施,包括RMSE、MAE、MAPE、DS、NADF和DM测试,表5显示了采用这些措施的所有模型的布伦特和WTI原油价格的结果。
表5显示了布伦特和WTI原油价格的所有模型的RMSE,图10中绘制了更清晰的图片,在所有模型中,EEMD(SD)-ARIMA-KF在两个市场中都取得了最低值(最好)。
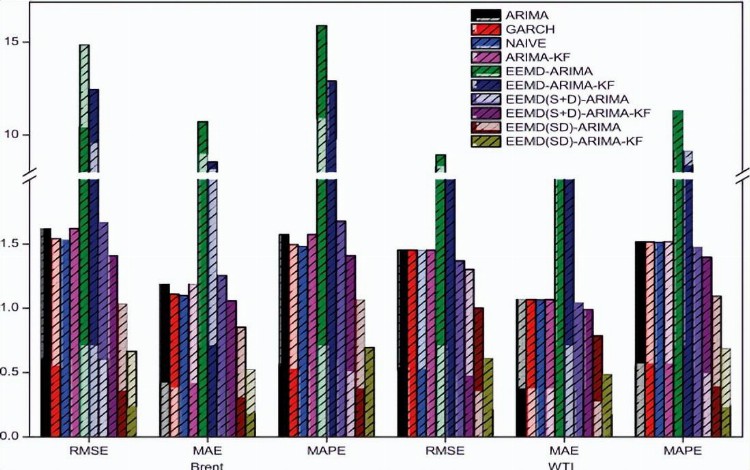
图10 不同模型对WTI和布伦特原油价格的RMSE、MAE和MAPE图
MAE是为布伦特和WTI原油价格的所有模型计算的预测评估标准的另一种度量,如表5所示并绘制在图10中;从MAE得出的结论与RMSE没有什么不同;EEMD(SD)-ARIMA-KF模型在两个市场上都取得了最低值,并且优于所有其他基准模型。
作方向性预测更为重要,因为投资者和政策制定者总是在寻找市场价格上涨或下跌的趋势;关于定向预测,单一模型ARIMA和GARCH的DS值显示在表5中并绘制在图11中两种原油价格都在51.14–53.13的范围内,非常接近随机猜测。
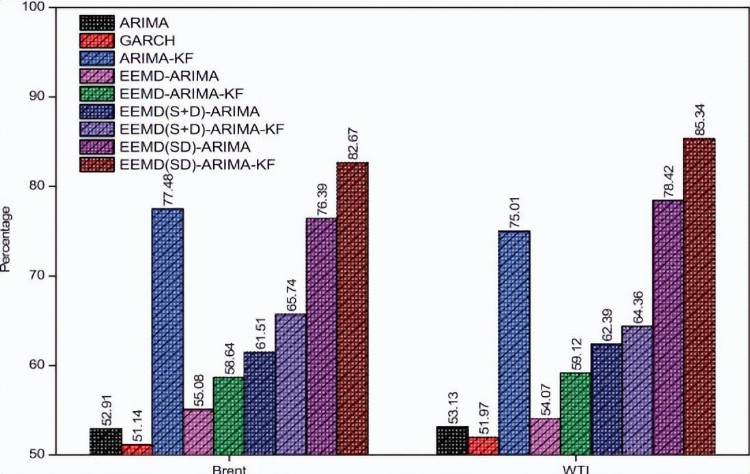
图11 不同模型对WTI和布伦特原油价格的DS图
下一个衡量标准是准确方向预测(NADF)的数量,模型EEMD(SD)-ARIMA-KF的NADF分别为布伦特和WTI原油价格的1817/2200和1385/1623,如表5和图12所示; 这是所有其他模型中最高的NADF,ARIMA、GARCH、NAÏVE、EEMD-ARIMA和EEMD-ARIMA-KF模型的NADF预测范围分别为布伦特和WTI原油价格的1124–1289/2200和843–959/1623,非常接近随机猜测。
所以,这五个模型并没有提供很好的方向性预测;EEMD(S+D)-ARIMA和EEMD(S+D)-ARIMA-KF模型的NADF在Brent和WTI原油价格的1353–1445/2200和1012–1044/1623范围内
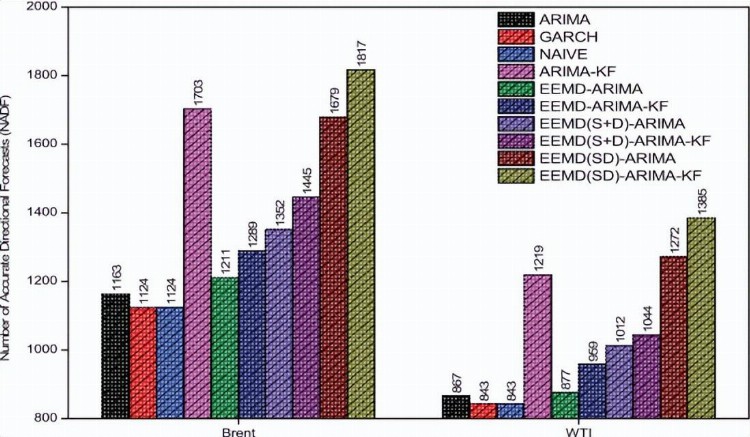
图12 WTI和布伦特原油价格的不同模型的NADF图
为了验证EEMD(SD)-ARIMA-KF模型的优越性,本研究还使用了DM检验,布伦特原油价格的DM检验统计值及其对应的p值(括号内)见表6,WTI原油价格见表7。
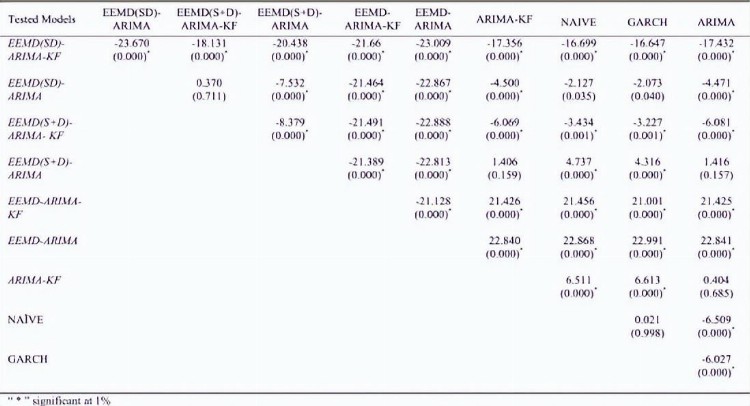
表6 布伦特原油价格的Diebold–Mariano(DM)测试结果
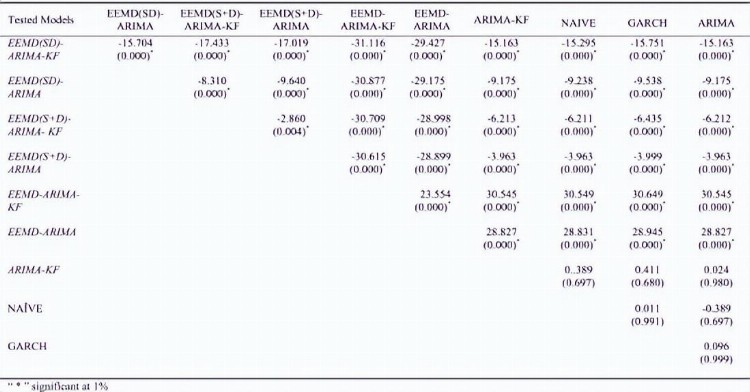
表7 WTI原油价格的Diebold–Mariano(DM)测试结果
将测试集的拟议模型EEMD(SD)-ARIMA-KF预测值与布伦特和WTI原油价格的原始值作图,ARIMA、ARIMA-KF和EEMD(SD)-ARIMA模型预测值也绘制在布伦特和WTI每日原油价格的图13中。
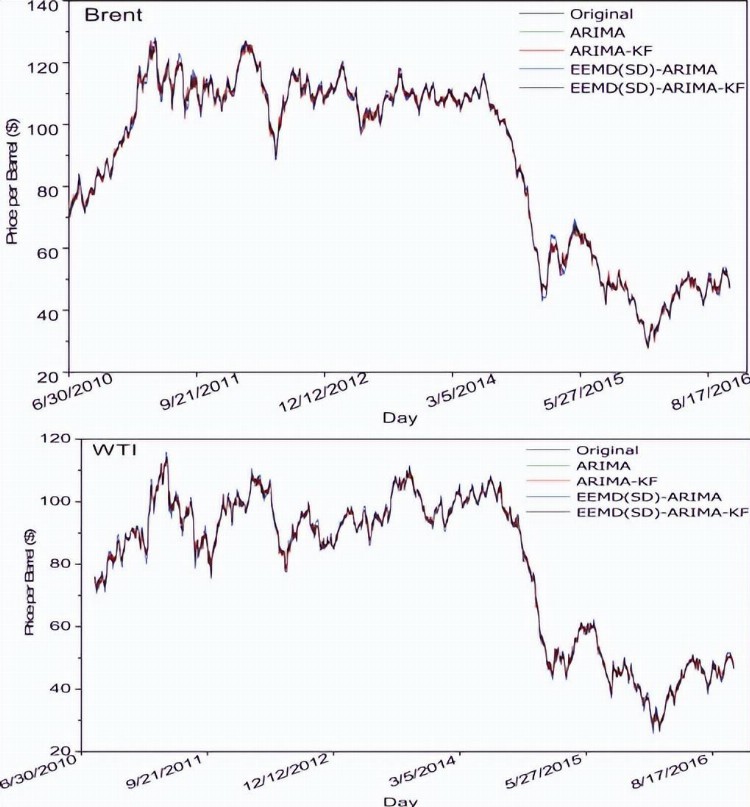
图13 布伦特和WTI原油价格不同模型的原始值和预测值
从以上结果和分析,我们可以得出以下结论:
尽管基于卡尔曼滤波的混合模型优于统计模型,但由于非线性和非平稳性,单一统计模型ARIMA、GARCH和NAÏVE无法在原油价格上取得令人满意的结果。
由于将模式重构为相对简单的组件的策略,与单个和没有RDE模型相比,具有重构模式的基于KF的集合模型显着提高了预测精度,即随机性和确定性。
所提出的EEMD(SD)-ARIMA-KF在RMSE、MAE、MAPE、DS、DM测试和NADF方面优于比较模型。
实验结果表明,将模式重构为随机和确定性分量是一种非常有效的方法,用于在集合模型中预测原油价格。
结论和未来的工作
提出了一种混合EEMD(SD)-ARIMA-KF方法来提高原油价格的预测精度;为了证明所提出模型的性能,我们将其与流行市场WTI和布伦特原油价格的最先进方法进行了比较。
实验结果表明,所有方法;ARIMA、GARCH、NAÏVE、ARIMA-KF、EEMD-ARIMA、EEMD-ARIMA-KF、EEMD(S+D)-ARIMA、EEMD(S+D)-ARIMA-KF、EEMD(SD)-ARIMA和EEMD(SD))-ARIMA-KF是有效的。
然而,所有预测精度指标RMSE、MAE、MAPE、DS、NADF和DM测试表明,混合模型EEMD(SD)-ARIMA-KF方法是高精度预测世界原油价格的最有效程序。
新的混合模型方法的优点是单独处理随机固有模式函数的结果,其中ARIMA模型的线性和非线性部分由卡尔曼滤波器组合以处理随机不确定性。

参考文献
L.Yu、Y.Zhao和L.Tang,“基于压缩传感的原油价格预测人工智能学习范式”,能源经济学,卷46,第236-245页,2014年11月。
X.Zhang、L.Yu、S.Wang和KKLai,“估计极端事件对原油价格的影响:一种基于EMD的事件分析方法”,EnergyEcon,卷31,第768-778页,2009年。
K.He、L.Yu和KKLai,“使用小波分解集成模型进行原油价格分析和预测”,能源,卷46,第564-574页,2012年。
如果你也喜欢我的文章,不妨点个“关注”吧!小生在此谢过了!
END


