赌神的万能公式

本文的“下注”是指合规游戏或合法投资，凡所有赌博都不值得参与。

一、三个故事

故事1：最后一口水

有个人在沙漠上迷路了，后来没有水，在救援人员赶来之前不幸离世。后来救援人员发现他随身携带的钢笔里还有墨水。有人说，假如他喝了墨水，没准儿能坚持到获救。

故事2：最后一层楼

这个故事大约是本世纪初我听到的。有个富豪，生意做得很大。后来遭遇挫折，亏光所有资产。绝望时突然想起自己在HK买过一层写字楼，一直没放在心上，这时候真成了东山再起的筹码——幸好忘了，不然可能连这层楼也亏掉了。

故事3：最后一笔财

和几个做投资的朋友吃饭。有位兄弟说起应该像当年犹太人那样，备一些应急的珠宝。一是如上世纪初地球混乱时能当买路钱，二是逃到生地后也需要重振旗鼓的本钱。‍‍‍‍‍‍‍‍‍‍‍‍‍‍

我提及以上三个故事，重点不在应急，而是想说：

任何时候，确保自己还有下注的能力，是一种极其重要的生存智慧。

这三个故事都揭示了一个核心的生存和成功原则：

无论你面对何种情况，都要确保自己保有下一步行动的能力，无论是在商业、投资还是生活中。

故事一中的人如果意识到自己的钢笔中的墨水，就可能能够继续生存下去，等待救援。

故事二中的富豪，在他的生意倒塌后，由于他之前在香港的一处写字楼，他有机会重新开始，再次积累财富。

故事三中的犹太人，他们储备了珠宝等贵重物品，使他们在最糟糕的情况下仍有生存的可能。

所有这些故事都强调了保持“下注”的能力的重要性：

1. 在投资中，这意味着你要保证自己有足够的资金和资源来应对市场的波动和不确定性；

2. 在生活中，这可能意味着你需要保持自己的身心健康，保持学习和进步，以便在面对困难和挑战时，你有能力和信心去应对。

二、“赌神”的第一公式‍‍

孤独大脑：说起下注，今天我们来聊凯利公式。据说这是赌神的“第一公式”......

ChatGPT：凯利公式是一个用来决定最优投注比例的公式，它帮助投资者和赌徒最大化长期的收益。

这个公式是由凯利在1956年提出的，他在贝尔实验室工作，试图找到一种有效的通信线路噪声管理策略。

然后他发现，他的理论可以应用于赌博和投资领域，帮助人们确定每次下注的最佳金额。

凯利公式如下：

f* = (bp - q) / b

这里：

• f* 是应该下注的资金的比例；
• b 是每次赌注的净收益率（赔率 - 1）；
• p 是获胜的概率；
• q 是失去赌注的概率，也就是（1-p）。

这个公式基于一个假设，那就是你可以准确估计获胜的概率和每次赌注的潜在收益。如果你的预测是准确的，那么凯利公式可以告诉你应该把多少钱投入到每次下注中，以最大化长期的收益。

然而，值得注意的是，凯利公式的应用在实际情况中可能会非常复杂，因为：

1. 我们很难精确地预测获胜的概率和每次赌注的潜在收益。

2. 凯利公式可能会导致比较大的投注比例，如果你不能接受这种风险，那么你可能需要把下注比例降低一些。

孤独大脑：讲起凯利公式，我们必须要提一下香农和索普。

当年索普发现了在赌场玩儿二十一点战胜庄家的办法，但是，即使胜率占优，期望值为正，因为赌场的本金相对赌徒几乎是无限多，所以每次如何下注依然是个难题。‍‍‍‍‍‍‍‍‍‍‍‍‍‍

索普向贝尔实验室最聪明的香农求助，香农于是推荐了第二聪明的凯利提出的公式。‍‍‍‍‍‍‍‍‍‍‍‍

ChatGPT：这个故事很有趣。

索普是一个极其聪明的数学家，他是最早系统性地研究二十一点游戏策略的人。他发现了一种可以在长期内战胜赌场的策略，这就是现在被广泛使用的“基本策略”和“计数系统”。

然而，索普在确定每一局应下注多少时遇到了问题。他明白，即使他有优势，但如果他每次下注过多，那么他仍然有可能在短期内输掉所有的钱。他需要一种方法来平衡胜率和下注金额。

于是，他找到了香农求助。香农是信息论的创始人，他认识到索普的问题实际上是一个关于信息和噪声的问题，于是推荐了凯利公式给他。

使用凯利公式，索普可以确定每次下注的最佳比例，使他的长期收益最大化。

凯利公式基于的思想是，如果你的策略具有正的期望收益，那么你应该适度地增加投注，但又不能过度，以免风险太大。

这个故事是一个完美的例子，展示了数学、信息论和决策理论是如何在现实中发挥作用的。

三、凯利公式的推导

孤独大脑：请你从数学角度，讲一下凯利公式的原理、推导。

ChatGPT：凯利公式的基本思想是最大化长期投资的复利增长。它是在特定假设下推导出来的，主要用于确定在有正期望值的投资或下注中应投入的比例。

先说原理。

凯利公式的基本思想源自信息理论和概率理论。它的目标是找到一个投资策略，使得资本的长期复利增长率最大。这通常涉及到在风险和收益之间进行权衡。

以下是公式推导。在一个简单的赌博游戏中，假设：

• 每次赌博赢得的概率为p；
• 输的概率为q=1-p；
• 每次赢得的收益率为b（赔率）；
• 每次输的收益率为-1（输掉的是你投入的资本）。

如果你决定每次赌博投入总资本的f比例，那么每次赌博后你的资本变为：

• 赢：(1+f*b)；
• 输：(1-f)。

假设每次赌博是独立的，那么在n次赌博后，你的资本Cn为：

Cn = C0 * (1+f*b)^X * (1-f)^Y，

其中，X是你赢的次数，Y是你输的次数。

在长期来看（即n趋于无穷大），资本的期望对数增长率（即对数资本的期望增长率）是最重要的指标。在这个模型中，这个增长率g为：

g = E[ln(Cn/C0)]/n = pln(1+fb) + q*ln(1-f).

你的目标是找到一个f，使得g最大。这可以通过求解上面这个式子的最大值来实现。

使用微积分的方法，你会找到：

f* = (bp - q) / b，

其中f*是使得g最大的f值。

四、不确定情况下的复利‍‍

孤独大脑：在某种意义上，凯利公式是用来计算不确定情况下的复利回报的。

在确定性情况下，复利的计算很简单；但在现实世界里，投资者哪怕胜率占优，也是有输有赢的。如上计算，全面考虑了亏和赚对整体收益的影响。

ChatGPT：是的，你的理解是正确的。

凯利公式就是在处理这样的问题：在一个存在风险的环境中，你应该如何分配你的投资，以最大化你的长期复利回报。

在确定性的环境中，复利的计算是简单直接的。如果你知道你的投资回报率，你可以简单地将这个回报率应用于你的投资本金，然后持续复利，得到你的最终回报。

然而，在现实世界中，投资者面临的通常是一种风险环境，即使你的策略胜率占优，你也不能保证每一次投资都会赢。

这就是凯利公式的应用场景。

凯利公式告诉你在每一次投资中应该投入多少本金，这个数值是根据你的胜率和赔率计算出来的，以期最大化你的长期复利回报。

当你遵循凯利公式进行投资时，即使在一段时间内有输的投资，只要你的策略在长期中胜率占优，你的投资本金将会按照复利增长。

然而，需要注意的是，凯利公式并不能消除风险，它只是提供了一个理论上的最佳投资比例，以期望在长期中获得最大的复利回报。

在实际应用中，投资者可能需要考虑到其他的风险因素，比如市场的波动性，投资者的风险承受能力等，所以可能不会完全按照凯利公式的建议进行投资。

孤独大脑：确切说，凯利公式只适用于期望值为正的投资。

也就是说，这个公式只能帮助一个好的投资，而无法挽救一个差的投资。

确切说，凯利公式无法帮助一个赌徒。

ChatGPT：是的，凯利公式是在投资或下注的期望值为正的情况下才能提供最优策略的。

期望值是每次投资可能的收益与各自发生的概率的乘积之和。

如果一个投资的期望值为正，那就意味着在长期内，这个投资平均每次能带来正的收益。

反过来，如果一个投资的期望值为负，那就意味着在长期内，这个投资平均每次会带来损失。

凯利公式的目标是找到一个策略，使得你的资本的长期复利增长率最大。

如果一个投资的期望值为负，那么无论你投入多少资本，长期来看你的资本都会减少。

在这种情况下，凯利公式没有意义，因为没有任何策略能增加你的资本。

因此，凯利公式必须基于期望值为正的投资，否则，它无法提供有效的投资策略。

五、赔率和胜率的错觉

孤独大脑：一篇强调“高赔率投资”的文章里，举了一个“反面”例子。

按照凯利公式：

1. 一个10倍赔率的机会，如果只有10%的概率赢，最佳下注仓位只有1%；

2. 一个0.5倍赔率的机会（赚1亏2），如果有80%概率赢，最佳下注仓位可以到40%。

该文由此认为： 经典投资理论更倾向于进行高概率的投资，能够提高对概率的把握就是提高胜率。

按照（凯利公式）这套重概率（胜率）轻赔率的做法，想在投资实践中获得高收益是非常不容易的。

因为概率很难预估，并且由于投资并非扔骰子式的大规模重复，对结果无法验证。

问题来了，凯利公式真的“重胜率轻赔率”吗？

ChatGPT：凯利公式是基于投资的概率和赔率来确定最佳的投资仓位的，所以它并非是“重胜率轻赔率”或“重赔率轻胜率”，而是二者都要考虑。我们来具体计算一下你提供的两个例子：

1. 对于一个10倍赔率的投资机会，如果你赢的概率是10%，那么根据凯利公式：F* = p - q / b = 0.1 - 0.9 / 10 = 1%。

这就是说，如果你想最大化你的长期收益，那么你应该把你的1%的资金投入这个投资机会。

2. 对于一个0.5倍赔率的投资机会，如果你赢的概率是80%，那么根据凯利公式：F* = p - q / b = 0.8 - 0.2 / 0.5 = 40%。

这就是说，如果你想最大化你的长期收益，那么你应该把你的40%的资金投入这个投资机会。

以上两个例子清楚地表明，凯利公式并不是“重胜率轻赔率”，而是同时考虑了胜率和赔率来确定最佳的投资仓位。

孤独大脑：其实有个简单的办法。

为了让人们理解凯利公式计算的是最佳结果，我们假设上面的第一个例子里，下注比例分别调整为2%，10%，和20%。然后对比1%的最佳建议下注比例，看看最终整体回报分别是多少。

ChatGPT：我们分别算算看就知道了。

如果我们以1%的下注比例进行投资，每次投资成功，收益是初始金额的10%，失败则损失初始金额的1%。

假设有10000次独立投资机会，其中有10%的机会获胜（1000次），90%的机会失败（9000次）。

在这种情况下，最终的资金状况如下：

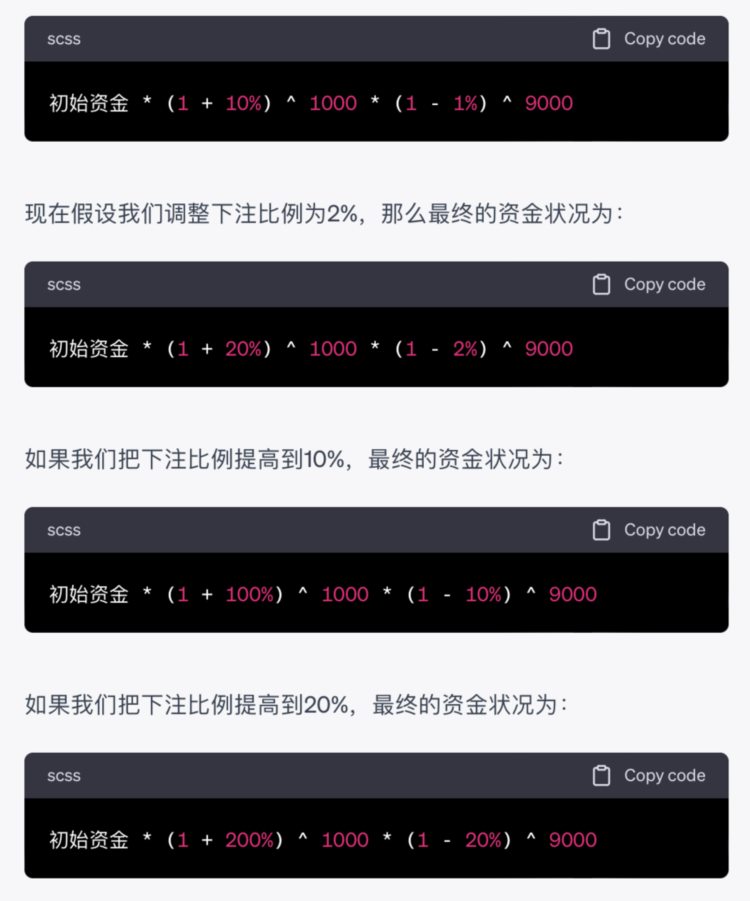
在如上四种情况下，按照凯利公式1%的下注比例将会得到最大的最终资金。

当你增加下注比例，尽管短期内可能看到更高的回报，但由于下注更多，每次失败时的损失也会更大，因此长期来看，最终的复利增长率将会降低。

孤独大脑：从直觉上看，似乎凯利公式偏好胜率高而赔率一般的投资，而对赔率高但胜率低的投资比较冷静。

ChatGPT：这是一个常见的误解，但实际上凯利公式并不偏爱胜率高的投资。

凯利公式的重点是找到最佳的下注比例，以最大化长期的复利增长。这个比例取决于两个因素：胜率和赔率。

在一个特定的赌局或投资中，赔率和胜率是相互关联的。较高的赔率通常意味着较低的胜率，反之亦然。凯利公式会考虑这两个因素，寻找一个平衡点，使得你的长期复利增长最大化。

实际上，如果赔率很高但胜率很低，凯利公式可能会建议你押注较小的比例，因为这样可以降低你因为连续失败而破产的风险。

相反，如果赔率较低但胜率较高，凯利公式可能会建议你押注较大的比例，因为你有较大的机会赢得这场赌局。

因此，凯利公式并不偏爱胜率高的投资，它只是试图在胜率和赔率之间找到最佳的平衡，以最大化你的长期复利增长。

孤独大脑：从人对下注比例的错觉看，人类在赌博的时候其实是有很大风险偏好的，这倒是很有趣。所以投资的时候谨慎一些总是好的。‍‍‍‍‍

六、“成长型”下注

孤独大脑：假如一个下注游戏是不断优化的过程，前半截是期望值为负，但不断下注会优化胜率，直至期望值为正。请问这类游戏如何使用凯利公式？

ChatGPT：对于这种情况，可以将整个游戏过程看作是两个阶段，并分别对这两个阶段应用凯利公式。

在第一阶段，期望值为负。在这个阶段，根据凯利公式，你应该减小你的投入，甚至可以选择不参与，以尽量减少损失。同时，你可以寻找改进策略的方法，比如学习新的技巧，获取更多的信息，以提高你赢的概率。

在第二阶段，你已经优化了你的策略，期望值变为正。此时，你可以根据凯利公式，计算出最优的投资比例，并据此进行下注。

这种策略假设你可以准确地估计每个阶段的期望值，以及你有足够的资源来经受第一阶段的损失。

在实际应用中，这可能是一种挑战，因此需要谨慎考虑是否有其他的风险管理策略，如止损、分散投资等。

孤独大脑：但第一个阶段不参与，就无法进入第二个阶段，请问该怎么办？

ChatGPT：这是一个复杂的问题，因为你的决策需要权衡短期的损失和长期的收益。在这种情况下，你可能需要做一些调整：

1. 分配一部分资金用于“学习”阶段。在期望值为负的初期阶段，你可以将这视为一种学习或优化的过程。你可以预先设定一个“学习预算”，并准备在这个阶段可能会有损失。这部分的资金应该是你愿意并能够承受损失的。

2. 逐步提高投资。当你的技能提升，胜率提高，期望值逐渐提高时，你可以逐渐增加你的投资，直到达到凯利公式推荐的最优投资比例。需要注意的是，你应该确保你的胜率确实有提升，并且期望值确实已经转正。

3. 不断审视和调整。在整个过程中，你应该不断审视自己的策略和结果，确保你正在朝着正确的方向进步。如果发现自己的策略不起作用，或者损失超过了你预设的“学习预算”，你应该停下来重新考虑你的策略。

总的来说，在面对期望值会发生变化的投资或下注时，使用凯利公式需要更加小心和灵活。

你需要准备好在学习和优化阶段面临一些损失，并适时地调整你的投资比例。

孤独大脑：我们这里讨论的“第一个阶段”，是不是属于精益创业的价值假设和价值验证阶段？

ChatGPT：你的观察非常有趣，确实可以将这个两阶段过程与精益创业的某些阶段相对应。

在精益创业中，初期阶段通常被分为价值假设和价值验证。

在价值假设阶段，创业者会基于对市场和用户需求的理解，制定一个商业模式或产品方案。

然后在价值验证阶段，通过构建最小可行产品（MVP）并在目标用户中测试，来验证这个假设是否正确。

如果将这个概念应用到你的问题中，第一阶段的期望值为负的游戏，可以看作是一个“价值假设”阶段。

你正在通过参与游戏，学习规则，试错，收集数据，以尝试找到一个有利可图的策略或技巧。

这个阶段可能会有一些损失，就像创业初期可能需要投入一些成本进行市场调研和产品开发。

然后，当你找到了一个可能赢的策略，就进入了“价值验证”阶段。

你开始实施你的策略，看看它在实践中是否有效。

如果你的策略确实提高了胜率并使期望值转为正，那么你就找到了一个有效的策略，就像创业者找到了一个有效的商业模式。

所以说，这个两阶段过程的确有一些与精益创业相似的地方。

但请注意，这只是一个类比，两者之间还有很多区别。

例如，创业过程中的许多因素，如市场竞争、客户反馈、技术更新等，在游戏或投资中可能并不适用。

孤独大脑：那么，我们上面说的第二个阶段，对应的是精益创业的哪个阶段？

ChatGPT：第二个阶段，即期望值为正的阶段，可以对应到精益创业的持续优化和扩大规模阶段。

在这个阶段，创业者已经验证了他们的价值假设，也就是说他们已经找到了一个满足市场需求的产品或服务，并已经找到了一条有效的商业模式。

然后，他们需要在这个基础上继续优化产品或服务，提高产品质量，增强用户体验，以提高客户满意度和用户留存率。

同时，他们也需要开始扩大规模，拓展市场，吸引更多的客户，增加销售额，以实现更大的商业成功。这可能包括增加营销和销售活动，扩大生产规模，拓展到新的市场，甚至寻找新的收入来源。

同样地，在第二个阶段的游戏或投资中，你已经找到了一个有利可图的策略，然后你需要在这个基础上继续优化你的策略，提高你的胜率，以提高你的收益。

同时，你也可能需要开始扩大投资规模，投入更多的资本，以实现更大的收益。

总的来说，这个阶段的主要目标是在验证了价值假设后，实现持续的优化和扩大规模，以实现更大的成功。

七、亏和赚的不对称‍‍‍

孤独大脑：我们说回凯利公式吧，它的目标是最大化长期的复利增长。

如果算到每年，其实就是最大化每年的复合回报率，也就是最大化期末财富的几何平均值。

ChatGPT：你的理解完全正确。凯利公式的目标就是最大化长期的复利增长，换句话说，它试图找到一个投资策略，使得在长期内你的期末财富的几何平均值达到最大。

这是因为，在投资中，我们对复利回报非常感兴趣，因为复利回报是资产增长的关键驱动力。

这一点很重要，因为许多投资者可能会犯一个常见的错误，那就是关注算术平均回报，而忽视了几何平均回报。

算术平均回报可以给出一种投资策略在每个时期的平均收益，但是它并不能准确反映一个投资策略的长期表现。

反之，几何平均回报更能准确地描述投资的长期增长，因为它考虑了资产价值的复利增长。

因此，凯利公式的目标就是找到一个策略，使得期末财富的几何平均值最大。这通常意味着它会建议投资者在面对有利的机会时增加投资，而在面对不利的情况时减少投资。

这是一种动态的投资策略，需要投资者在每个时期都根据当前的胜率和赔率来调整投资比例。

孤独大脑：我们讲一下几何平均回报和算术平均回报之间的差别吧。

ChatGPT：好的，来看一个简单的例子。

假设你有一个投资，第一年你赚了50%，第二年你亏了50%。让我们看看算术平均回报和几何平均回报是如何计算的。

算术平均回报很简单，你只需要把每年的回报相加然后除以年数。在这个例子中，算术平均回报就是（50% - 50%）/ 2 = 0%，看起来你没有赚也没有亏。

然而，如果我们真正地去看你的投资表现，情况就不是这样了。假设你初始投资了100元，第一年你赚了50%，所以你有150元。第二年你亏了50%，那么你就只剩下150元的50%，即75元。实际上，你在这两年里亏了25元。

这时候，你需要计算的是几何平均回报，也就是每年投资的复合增长率。在这个例子中，几何平均回报是（75/100）^（1/2） - 1 = -13.4%，这意味着每年你平均亏损了13.4%，这才是反映你真实投资表现的指标。

这个例子清楚地表明，当我们关注投资的长期表现时，几何平均回报（也就是复合年化回报率）比算术平均回报更能准确地反映投资的真实收益。

这也是为什么凯利公式的目标是最大化几何平均回报，而不是算术平均回报。

孤独大脑：显然，我们一生的财富复利，是一个连续相乘的过程。所以，涨50%与跌50%并不对称。

ChatGPT：你说得对。

我们在计算投资收益时，涨50%和跌50%并不对称，这是因为投资收益是按照复利计算的，而不是简单地相加或相减。

这就是为什么几何平均回报（反映