贴现和利息是金融领域中相关但不完全相同的概念。它们在时间价值和资金流动性方面有不同的应用和含义。
- 贴现(Discounting):贴现是将未来的现金流或款项按照一定的折扣率提前换算成现值。在贴现的过程中,使用的折现率通常反映了资金的时间价值和风险。贴现可以用于债券定价、投资决策和贷款评估等方面。
- 利息(Interest):利息是指在一定期间内根据利率产生的收益或费用。利息通常与借入或投资资金的使用有关。在贷款和债券领域,利息是借款人或债券发行人向贷款人或债券持有人支付的一种补偿。利息可以是固定的,也可以根据一定的利率计算方法(如复利)而变化。
虽然贴现和利息都涉及到未来现金流的计算和现值的概念,但它们的应用和意义略有不同:
- 贴现是将未来现金流按照一定的折扣率提前换算成现值,以评估其当前价值。贴现用于确定未来现金流的现值,考虑时间价值和风险因素,从而进行决策和定价。
- 利息是根据一定的利率计算,在一定时间期间内产生的收益或费用。利息通常涉及到借款、投资或债券等情境中的资金使用和回报。
贴现和利息之间的关系取决于具体的情境和金融工具。在一些情况下,贴现可能包含了利息的计算,但在其他情况下,它们可以是分开考虑的概念。在实际应用中,根据具体情况和需要,可以结合考虑贴现和利息的概念来进行综合分析和决策。
1、贴现和贴现率
通常,利息支付的方式有两种:
- 一种是期末支付,它是本金的增加值。如,年初存入银行100元,一年后到期获得5元利息,它就是100元本金的增加值,且在年末支付。这种利息称为滞后利息或期末付利息;
- 另一种是期初支付,它是积累额的减少额,这种利息称为贴现。如,购买面额为100元的一年期国债,现时支付90元即可,则本期国债的利息为10元,它是在100元基础上的减少额,10元利息在购买时就已获得,10元称为贴现额。
贴现率用来衡量贴现水平,它是单位货币在一定时期内的贴现额。用符号d 表示贴现率,第t 个时期的贴现率为:
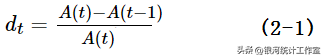
用积累函数表示为:

在复利条件下,如果利率不变,有,
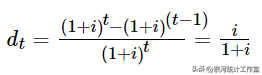
上式表示常数贴现率与常数利息率的关系为:
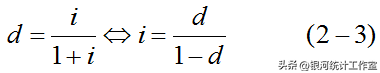
在常数贴现率条件下,积累额为,

【例2.1】计算1998年1月1日1000元在复利贴现率5%下1995年1月1日的现值及利息率。
解:1995年1月1日的现值为,
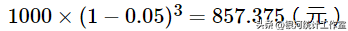
年利息率为,
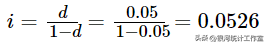
2、名义贴现率
名义贴现率符号表示为,

m为结算次数,每次结算的实际贴现率为

则有,
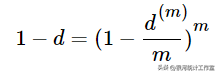
解得,
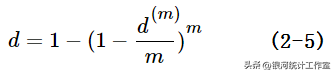
或者,
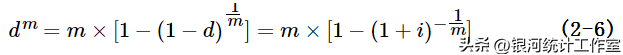
3、名义利率和名义贴现率的关系
由(2-3)贴现率与利息率关系式和(2-5)可得,
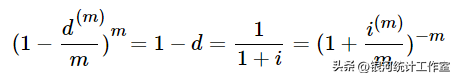
整理得,
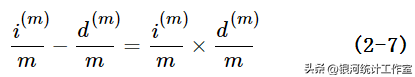
转换为,
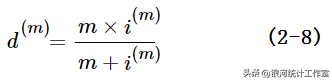
或,
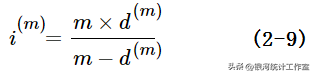
一般地,如果一年支付m次利息的名义利率、一年支付n次贴现的名义贴现率,年初的本金为1,则年末的累积额有,
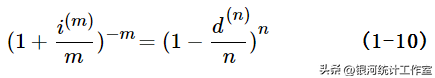
转换为,
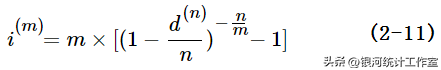
或,
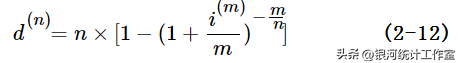
【例2.2】某人以每年3.6%的利率从银行贷款1000元,在复利条件下按月结算,3年后欠银行多少钱?
解:按月结算时,年利率3.6%,月利率为0.3%。3年36个月的欠款额为:
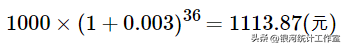
名义利率,
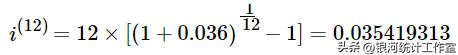
名义利率计算的3年36个月欠款额为,
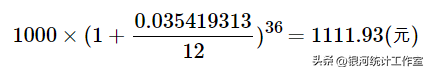
【例2.3】
a、求每月结算的年利率为12%的实际利率;
b、求每季结算的年贴现率为10%的实际贴现率;
c、求相当于每月结算的年利率为12%的半年结算的贴现率。
解:
a、 实际利率为:
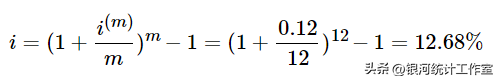
b、 实际贴现率为:
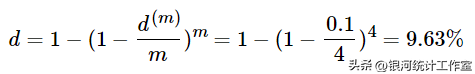
c、由式(2-12):
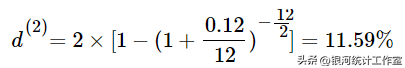
贴现将未来的现金流或款项按照一定的折扣率提前换算成现值。这个过程可以应用于债券、贷款、投资等各种金融交易中。
贴现的基本原理是时间价值的概念,即未来的一笔款项或现金流由于存在时间价值,其价值会随着时间的推移而降低。因此,为了提前获得这笔款项或现金流的价值,可以按照一定的折扣率进行贴现。
在贴现过程中,使用的折现率(贴现率)通常是根据市场条件和风险评估来确定的。较高的折现率表示较高的风险或较低的预期回报,从而导致贴现后的现值较低。
贴现应用在如下领域:
- 债券市场:债券的面值和利息支付通常是未来的现金流。投资者可以将这些未来现金流按照当前市场利率进行贴现,以确定债券的当前价值。
- 贷款和融资:贴现可以用于确定未来贷款或融资的现值。借款人可以使用贴现来计算贷款的净现值,以评估是否接受贷款条件。
- 投资决策:在进行投资决策时,贴现可以帮助评估项目的净现值。通过将项目的未来现金流贴现到现值,可以比较投资回报与风险,并作出决策。
贴现是金融领域的一个复杂概念,具体应用和计算方法可能因不同的情境和金融工具而有所不同。在实际运用中,可能需要考虑其他因素,如通胀率、风险溢价等。


